Sorter koralików z siecią neuronową na Arduino Nano

Na skróty

1. Cel projektu

2. Hardware

3. Software

4. Podsumowanie

5. Możliwości zmian

6. Pliki do pobrania (downloads)

7. Filmik prezentujący działanie sortera

Cel projektu

Znacie ten problem? Przychodzi do Was 10-letnia córka i prosi, żebyś jej pomógł w posortowaniu koralików. No jasne, i siedzisz kilka godzin... czerwony do czerwonych, niebieski do niebieskich, różowy do różowych... masz już trzy! Zostało jeszcze jakieś... 22 tysiące!!!

Właśnie to jest ten problem, który chciałem rozwiązać :). Koncepcja: wrzucam koraliki do maszyny, maszyna sortuje koraliki, a my w tym czasie możemy porobić coś innego.

Zrobiłem rozeznanie w internecie, żeby sprawdzić jak inni poradzili sobie z tym kłopotem. Okazuje się, że problem jest dość powszechny :) a podejścia do jego rozwiązania są różnorakie: detektor oparty na smartfonie (Aaron Christophel), system oparty na Arduino (Mac Electronic) - fajne, bo relatywnie szybko sortuje koraliki. Nablanos skonstruował system podobny do układu Aarona, ale na Arduino - i działa znacznie szybciej.

Zainspirowany różnymi rozwiązaniami, skonstruowałem własny sortownik - nie jest w niczym lepszy od innych rozwiązań, chciałem po prostu wykorzystać komponenty, które miałem pod ręką. To co wyróżnia tę konstrukcję to zastosowanie sieci neuronowej do analizy koloru, którą udało się upchnąć w małym Arduino Nano na chipie ATmega328P! Więcej o tym w części Software.

Hardware

Cały sorter od strony mechanicznej zaprojektowałem w Autodesk Fusion 360. Poniższy rysunek pokazuje urządzenie oraz jego rozmiary.

Rys. 1. Sorter koralików.

Sorter składa się z pojemnika na nieposortowane koraliki (10), mechanizmu pobierania i detekcji danego koralika (20), który następnie przemieszcza się do przez zespół rurek (30) do 1 z 9 pojemników (40). Całość sterowana jest płytką Seeeduino - odpowiednik Arduino Nano zamkniętej w obudowie (50). Cały sorter jest nieduży i zajmuje ok. 25cm przestrzeni na biurku. Pojemnik sortera pomieści ok. ~1500 koralików.

Zależało mi na minimalistycznej konstrukcji. Jest to okupione tym, że sorter może w danej sesji posortować max. 8 kolorów, a pozostałe koraliki zrzuca do większego pojemnika. Te po pierwszej sesji muszą trafić ponownie do pojemnika (10) do dalszego sortowania.

System poboru koralika został oparty na podobnej zasadzie jak w rozwiązaniu Mac Electronic. Obrotowa tarcza jest odchylona o 20 stopni od pionu, dzięki czemu koraliki chętnie trafiają do otworu transportującego. Szczegóły rozwiązania przedstawia rysunek 2.

Rys. 2. Układ pobierania koralika

Stojan (21) posiada oś o średnicy 19,6mm na którą osadzone jest transportowe koło zębate (22) o 72 zębach i grubości 5 mm. Koło posiada 8 otworów transportujących o średnicy wlotowej 7,6 mm i wylotowej 9,3 mm. Dzięki temu, koralik znajdujący się nad otworem wyjściowym (25) uzyskuje dodatkowy impet (grawitacyjny) do przemieszczenia się rurką wylotową. Koło transportowe jest napędzane mniejszym kołem (23) o 10 zębach. Jest ono osadzone na ośce silniczka 5V o prędkości obrotowej 130RPM umieszczonym w komorze (28). Synchronizację położenia koła względem pozycji sensora (24) zapewnia układ diody nadawczej (27) w uchwycie (26) i fototranzystora (28) - patrz Rys. 3.

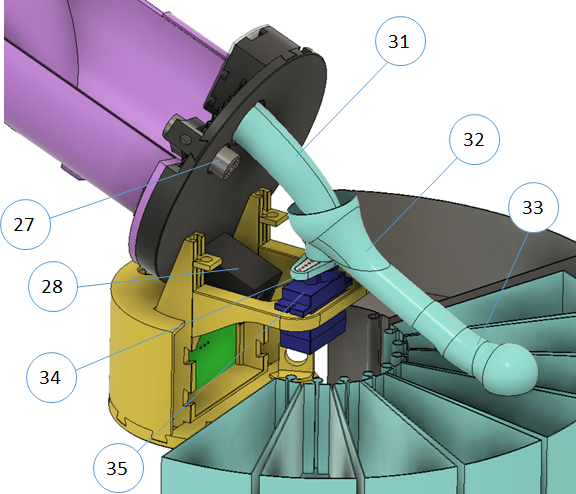
Rys. 3. Układ zrzutu koralika do odpowiedniego pojemnika

Po detekcji koloru koralika koło transportowe zatrzymuje się na czas ustawienia rurki zrzutowej (32) nad odpowiednim pojemnikiem zrzutowym. Następnie koralik przemieszczany jest do otworu zrzutowego (25) i rurkami (31), (32) i (33) trafia do odpowiedniego pojemnika. Rurka (32)+(33) jest osadzona poprzez adapter (34) na orczyku serwomechanizmu (35) o zakresie kątowym ok. 180 stopni.  

Elektronika

Schemat elektroniczny jest przedstawiony na Rys. 4.

Rys. 5. Schemat połączeń komponentów sortera

System sterowania oparty jest na płytce Seeeduino. Jest to kompatybilna płytka z Arduino Nano ze zwiększonym do 1A prądem stabilizatora napięcia 5V. Złącze IRPH zasila diodę IRED i doprowadza sygnał z fototranzystora do układu formującego sygnał cyfrowy zbudowanego na komponentach R2, R4, R5, Q1 i C2. W chwili oświetlenia fototranzystora na wyjściu tego układu pojawia się stan niski doprowadzony do wejścia D7. Ten sygnał pozwala programowi na zorientowanie się w pozycji otworu z koralikiem względem położenia sensora TCS. Fototranzystor i dioda IRED jest wymontowana z modułu odbiciowego (np. takiego). Ale można zastosować dowolny IRED i fototranzystor, oba w obudowie diody 5mm. Złącze SRV służy do podłączenia serwomechanizmu SG90 - najprostszy plastikowy jest wystarczający, gdyż nie pracuje tu pod obciążeniem. Sterowanie serwo odbywa się z wyjścia D9, jednego z dwóch wyjść PWM płytki Arduino. Moduł sensora kolorów TCS34725 jest podłączony do interfejsu I2C. Dodatkowe wyprowadzenie sterowania białą diodą podświetleniową jest podłączone do cyfrowego wyjścia D3. Silnik M1 to prosty silniczek 6V/130 RPM. Jest on kontrolowany przez moduł Pololu 2990 (układ DRV8838). Sygnał EN to drugie wyjście PWM z Arduino i steruje prędkością obrotową, a sygnał PH steruje kierunkiem obrotów. Silnik wysterowywany jest ok. połową zakresu sygnału PWM (~128 z 255), więc jego prędkość obrotowa podczas pracy wynosi ok. 60 RPM, dlatego można zastosować silnik z nominalną prędkością obrotową w zakresie 60-200 RPM. Opcjonalnie można zastosować też mały silniczek wibracyjny. Nie jest on krytycznym elementem i sorter działa również bez niego. Jego rola jest w przypadku, gdy koraliki czasem się tak ułożą lub gdy jest ich już bardzo mało, że przez kilka-kilkanaście obrotów koła transportowego nie chcą wskoczyć do otworów. Program wykrywa taką sytuację i włącza na chwilę ten silniczek powodując wibracje pojemnika z koralikami i zwiększa tym samym szansę wskoczenia koralików do otworów transportowych.

Całość została zmontowana na płytce uniwersalnej dwustronnej o rozmiarze 43 x 35 mm. Rozmiar płytki jest ważny, gdyż jest dopasowany do podstawy.

Rys. 6. Schemat połączeń komponentów sortera

Moduł Arduino oraz moduł sterownika silnika trzeba zamontować na listwach żeńskich do goldpinów - dzięki temu tworzy się przestrzeń do wlutowania tranzystora i niektórych rezystorów. Dodatkowo można będzie je wymienić, gdyby się przepaliły - ewentualnie wykorzystać w innym projekcie.  Złącza do podłączenia modułów wykonawczych zostały zamontowane po drugiej stronie płytki - zdjęcie 1.

Zdj. 1. Zmontowana płytka sterująca.

steruje Prędkość obrotowa nie jest tu krytyczna, może być 60-200 RPM jest chemacie jest widoczny microswitch, który ostatecznie nie był wykorzystany, więc jego montaż nie jest konieczny. Moduł diody IRED/Fototranzystor jest wykorzystany do zatrzymania silnika DC w chwili, gdy koralik znajduje się

Software

Sorter sterowany jest z klasycznego Arduino Nano z mikroprocesorem ATmega328P. Schemat blokowy programu sterującego przedstawiony jest na rysunku 7.

Rys. 7. Schemat blokowy programu sterującego

Po uruchomieniu programu w kroku S10 uruchamiany jest blok Setup, w którym ustawiane są wejścia i wyjścia sterujące, konfigurowany jest port szeregowy, ustawiane zmienne na pozycje początkowe, itp. Tuż przed zakończeniem bloku Setup program w kroku S20 sprawdza stan przycisku. Jeśli wciśnięty, program przechodzi do kalibracji S30, w przeciwnym razie rozpoczyna się pętla główna Loop. W kroku S40 uruchamiany jest silniczek napędowy koła transportowego - następuje pobranie i transport koralika. Ten blok analizuje jednocześnie stan sygnału z fototranzystora czekając na przejście ze stanu wysokiego do niskiego (linia wejściowa D7), po czym odlicza określony czas i przechodzi do kroku  S50. W tym kroku robimy 5 pomiarów wartości RGBC z czujnika koloru. Ponieważ czas akwizycji jest ustawiony na 24ms, zebranie 5-ciu pomiarów zajmuje ok. 120ms. Zbieranie tych pomiarów odbywa się podczas ruchu koła transportowego, więc koralik się nadal przemieszcza. Dzięki temu w kroku S60 możemy wybrać maksymalną wartość (analizując  wartość C, czyli sumaryczną wartość kanałów RGB -> patrz datasheet sensora TCS). Maksymalną zarejestrowaną wartość podajemy do modułu detekcji koloru koralika - krok S70. Funkcja detekcji koloru jest oparta o małą sieć neuronową - o tym opowiem w dalszej części artykułu. Po identyfikacji koloru program przechodzi do kroku S80, w którym przydziela jeden z dziewięciu pojemników. W początkowej fazie do pojemników 1-8 nie jest przydzielony żaden kolor (wartość -1), a do pojemnika o indeksie 0 jest przydzielony kolor NONE (indeks koloru = 0). Program sprawdza, czy aktualny kolor koralika został już przydzielony do któregoś z pojemników. Jeśli nie, przydziela go następnemu wolnemu pojemnikowi. Gdy wszystkie 8 pojemników zostało już przydzielone do różnych kolorów, jest to kolejny kolor, któremu przydzielany jest pojemnik zerowy, czyli ten największy. Wszystkie koraliki które tam trafiają wymagają sortowania w następnej sesji.

W następnym kroku S90 następuje pauza (funkcja delay) programu umożliwiając stoczenie się poprzedniego koralika przez rurkę spustową do danego pojemnika. Po pauzie program jeszcze sprawdza, czy wciśnięto przycisk, jeśli nie - w kroku S110 następuje ustawienie rurki spustowej nad odpowiedni pojemnik dla bieżącego koralika. W chwili gdy będzie mierzony następny koralik, bieżący zacznie staczać się do pojemnika.

Wciśnięcie przycisku w kroku S100 umożliwia przerwanie aktualnego sortowania (np. w celu opróżnienia pojemników) w kroku S120 oraz wysłanie na port szeregowy aktualnej statystyki zebranych koralików - krok S130. Kontynuacja programu następuje po ponownym wciśnięciu przycisku - S140. Jeżeli wciśniemy przycisk na dłużej niż 3 sekundy, aktualnie przydzielone kolory do pojemników zostaną wyzerowane i program wznawiając sortowanie przydzieli ponownie - tym razem już inne kolory - do kolejnych pojemników.

Osobnego omówienia wymaga moduł detekcji koloru na podstawie sygnałów RGB (krok S70). Zrealizowałem to w dwojaki sposób: 1) przez zwykłą statystykę, oraz 2) z wykorzystaniem prostej sieci neuronowej. Niezależnie od wybranego sposobu, w pierwszej kolejności należało zebrać sygnały dla różnych kolorów. W tym celu niestety trzeba było posortować ręcznie po kilkadziesiąt koralików z każdego koloru, a następnie gromadzić sygnały. Aby mieć pewność, z jakiego koloru pochodzą sygnały, trzeba wrzucać do sortowania koraliki tylko jednego rodzaju na raz. Zebrane dane (np. programem Realterm -> Capture) trzeba wczytać do programu EXCEL, a następnie usunąć te pomiary, które reprezentują pusty otwór (brak koralika), który niestety czasem się zdarza. Mając tak zebrane dane, możemy przystąpić do ich wykorzystania.

Pierwsze podejście: metoda statystyczna

Schemat działania w tym podejściu przedstawia poniższy rysunek.

Rys. 8. Metoda statystyczna. Górny wiersz: wyznaczanie modelu statystycznego, dolny wiersz: wykorzystanie modelu do progowania sygnału i określenia koloru bieżącego koralika.

Dane wejściowe w postaci szeregu zarejestrowanych sygnałów RGB wraz z nadaniem etykiety koloru (numer od 0 do 17 - patrz tabela 2) zostały poddane analizie statystycznej w Excelu: wyznaczana jest wartość średnia (Ave) oraz odchylenie standardowe (sigma) dla każdego kanału i każdego koloru koralika - Tab. 1.

Rys. 9. Zdjęcie koralików oraz odpowiadający im sygnał na detektorze TCS34725. Każdy kolor złożony jest z trzech wartości średnich R,G,B z tabeli 1.

Jak widać, sensor całkiem poprawnie rozpoznaje kolory, a średnie wartości RGB są poprawnie wyznaczone.

W fazie analizy koloru (Rys. 8, dolny wiersz) następuje detekcja bieżącego koralika. Wartości R,G,B i C są sprawdzane, czy mieszczą się w zakresie wartości średniej +/- 3*sigma. Jeśli wszystkie cztery wartości mieszczą się w danym przedziale, wskazywany jest indeks tego koloru. Niestety, taka metoda detekcji nie jest zbyt dokładna. Poniżej przedstawiłem wynik takiego podejścia w postaci  tabeli pomyłek (tzw. confusion matrix). 

Jak widać dokładność identyfikacji poszczególnych kolorów jest bardzo niska, całkowity wskaźnik dokładności wynosi ok. 55%, co jest bardzo słabym wynikiem. Wynika to z faktu, że poszczególne wartości R,G,B dość mocno się zmieniają w zależności od ułożenia koralika w komorze: albo koraliki leży (sygnał jest silniejszy), albo stoi (sygnał słabszy, gdyż mniejsza powierzchnia koralika odbija światło). Do tego też wpływ na sygnał mają indywidualne własności danego koralika (mogą pochodzić przecież z różnych partii). Dla przykładu, sygnał RGB dla dwóch zielonych koralików o najmniejszym i największym sygnale jest podany w tabeli 2. 

Tab.2. Sygnał minimalny i maksymalny dwóch różnych koralików zielonych oraz stosunki BR, BG i GR.

Widać wyraźnie w jak szerokim zakresie zmienia się sygnał dla tego samego koloru.

Z powyższego powodu dołączyłem do modelu statystycznego dodatkowe cechy - stosunki poszczególnych kolorów, które - jak się wydaje - powinny być bardziej niezmiennicze. W tabeli 2 są podane trzy stosunki kanałów RGB oznaczone jako BR, BG i GR, i są zdefiniowane tak, że BR = 100*B/R,  BG = 100*B/G,   GR = 100*G/R. W tabeli 1 można także znaleźć średnie wartości tych stosunków wraz z odchyleniami standardowymi dla wszystkich kolorów. Jak widać rzeczywiście zmienność tych stosunków jest znacznie mniejsza niż surowych sygnałów RGB. 

Po dodaniu do modelu statystycznego tych dodatkowych trzech cech (czyli BR, BG i GR) analizowanych jest łącznie 7 cech. Taki model sprawdza się nadspodziewanie dobrze, co potwierdza tabela pomyłek przedstawiona poniżej.

 

Rys. 11. Confusion Matrix dla metody identyfikacji kolorów poprzez klasyczne progowanie sygnału (7 cech: R,G,B,C,BR,BG,GR).

 

Jak widać wynik jest bardzo dobry, całkowita dokładność na poziomie 95%. Największe kłopoty są z rozpoznaniem koloru Lt Violet, który jest mylnie rozpoznawalny w 51% jako Violet. Dokładność rozpoznania koloru brązowego Brown jest także zaniżona, gdyż metoda myli go z brakiem koralika (czyli kolorem czarnym). Pozostałe kolory w większości mają rozpoznawalność na poziomie powyżej 90% .

 

Aby poprawić detekcję kolorów (zwłaszcza Lt Violet iViolet oraz None z Brown), warto przyjrzeć się zgromadzonym sygnałom dla wszystkich kolorów w trzech wymiarach - rysunek 12. Tu przedstawiłem je w przestrzeni trzech cech: BR, BG oraz C.

 

Rys. 12. Wykres 3D punktów pomiarowych dla wszystkich koralików w przestrzeni cech BR, BG i C.

 

Na wykresie 3D widać wyraźnie, że obie problematyczne pary kolorów tworzą wyraźnie rozdzielone chmury punktów przynajmniej w przestrzeni cech BR, BG i C. Można więc założyć, że da się skonstruować takie warunki na te cechy, aby można było poprawić ich detekcję. Aby to zrobić, należałoby skonstruować kilka lub kilkanaście kolejnych cech, np. B*R^2, B*R*G^3, może też B*pierwiastek(R*G), itp., itd. Jakie dokładnie funkcje i relacje tu użyć - można do pewnego stopnia przewidywać patrząc na wykresy 3D w tych cechach i starając się dobierać takie cechy, aby można było oddzielać liniami prostymi powstające chmury punktów. Jest to jednak metoda czasochłonna, wymagająca wielu prób i błędów.

 

I tu dochodzimy do drugiego podejścia.

 

Drugie podejście: sieć neuronowa NN

 

Z pomocą przychodzi tu zastosowanie sieci neuronowej, która sama - na podstawie danych treningowych - znajdzie sobie najbardziej optymalne cechy do rozdzielenia wszystkich chmur punktów jak najbardziej dokładnie.  Dodatkową inspiracją do użycia tutaj sieci neuronowej była chęć wykorzystania wiedzy, którą zdobyłem na fantastycznym darmowym kursie z podstaw sieci neuronowych autorstwa Andrew Ng dostępnym w serwisie coursera.org . Obecnie (styczeń 2023) dostępna jest zaktualizowana wersja tego kursu pod nazwą Machine Learning Specialization. Kurs prowadzony był z wykorzystaniem środowiska Octave (darmowa wersja Matlab), dlatego implementacja modelu sieci oraz jej treningu została zaadaptowana z kodów źródłowych właśnie w tym środowisku. 

Rys. 13. Metoda NN. Górny wiersz: wyznaczanie modelu NN, dolny wiersz: wykorzystanie modelu NN w procesie predykcji koloru bieżącego koralika.

Zastosowałem najprostszą sieć tzw. Fully Connected Network o architekturze 3x8x18, czyli 3 neurony warstwy wejściowej (do wprowadzenia wartości R,G,B - nie używałem wartości C, która jest po prostu sumą kanałów RGB), 8 neuronów warstwy ukrytej oraz 18 neuronów warstwy wyjściowej - czyli tyle ile kolorów jest do rozpoznania. Liczbę 8-miu neuronów warstwy ukrytej dobrałem eksperymentalnie. Zależało mi na jak najmniejszej sieci, aby cały model nie zabierał zbyt dużo pamięci w skromnych zasobach Arduino. Te 8 neuronów okazało się w zupełności wystarczające - można je interpretować jako 8 cech, które sieć w trakcie treningu sobie sama określiła.

Model sieci o budowie 3x8x18 zawiera dwie macierze wag, których wartości są aktualizowane w trakcie treningu. Są to:
Theta1 o rozmiarze [8, 4] - czyli 32 liczby typu single - wagi połączeń między warstwą wejściową a warstwą ukrytą , oraz

Theta2 o rozmiarze [18, 9] - czyli 162 liczby typu single - wagi połączeń między warstwą ukrytą a warstwą wyjściową.

Do treningu sieci wykorzystałem 70% wszystkich próbek ( 5072/7248), a do testów pozostałe 30% próbek.

Sieć szkoliła się przez 1000 epok, co zajęło jej ok. 20 minut na komputerze Intel Core i5-12400F, 16GB RAM.

Program w Octave uzupełniłem o część generującą odpowiednie macierze oraz zmienne w języku C, które można łatwo dołączyć do programu Arduino.

Przy architekturze sieci 3x8x18, sieć potrzebuje zaledwie 812 B pamięci programu oraz 44 B pamięci podręcznej na zmienne. 

Sama implementacja procedury predykcji siecią 3x8x18 nie jest skomplikowana - to po prostu mnożenie wartości przez wagi i sumowanie w odpowiedniej kolejności plus funkcja aktywacji sigmoid. Zgłębianie matematyki stojącej za siecią neuronową wykracza poza ramy tego artykułu, ale zainteresowanych odsyłam do kursu pana Ng. Cała predykcja na Arduino trwa tylko 10 ms. Definicja funkcji, która realizuje całą procedurę jest następująca

Funkcja przyjmuje wartości R,G,B. Ostatni parametr to wskaźnik do zmiennej w której funkcja zapisze wartość prawdopodobieństwa (0..100) przypisanego przez sieć zidentyfikowanemu kolorowi. Funkcja zwraca indeks danego koloru, tj. wartość z przedziału 0 do 17.

Na koniec przedstawiam confusion matrix dla bazy testowej.

Rys. 10. Confusion Matrix dla metody NN, sieć FCN o rozmiarze 3x8x18.

Jak widać udało się poprawić jakość rozpoznawania kolorów Violet oraz Lt Violet, a całkowita dokładność detekcji wzrosła do ponad 99%.

Podsumowanie

W tym projekcie udało się skonstruować sorter koralików w oparciu o Arduino Nano z wykorzystaniem sieci neuronowej. Wykazałem, że z sukcesem można zaprojektować efektywną sieć typu FCN do analizy sygnału z sensora kolorów, która doskonale radzi sobie z rozpoznawaniem 18 kolorów z dokładnością powyżej 99%, choć w tym przypadku również prosty model statystyczny z 7 cechami również sprawdzał się nadspodziewanie dobrze (95% skuteczności).

Słabą stroną konstrukcji jest część mechaniczna, która wymagałaby zmian. Niemniej urządzenie spełnia wymagania i realizuje sortowanie koralików.  

(C) TB.

Adaptacja do własnego sortera

1. Dopasowanie modelu sieci do własnego sortera dla tego samego zestawu kolorów koralików.

Dla innego sensora widmo jak i natężenie białej diody użyte w module sensora do oświetlenia koralika może się nieznacznie różnić. Dlatego wymagana jest kompensacja koloru białego. Kod w Arduino jest na to przygotowany - wystarczy policzyć średnią wartość dla kanałów R,G,B dla kilkunastu-kilkudziesięciu białych koralików w swoim własnym sorterze i wprowadzić je do stałej BS_wav na początku kodu Sorter.ino, np.:

const float BS_wav[] PROGMEM =

2. Dopasowanie modelu sieci do odmiennego zestawu koralików

Jeśli opcja 1 nie pomoże lub posiadasz inny zestaw koralików, musisz wygenerować swoje własne dane treningowe i użyć programu w Octave do wygenerowania modelu sieci. W tym celu należy zebrać min. po kilkadziesiąt danych z poszczególnych koralików i zapisać je w postaci tekstowej w formacie Red,Green,Blue,Cclear,Label. Przykład podano poniżej:

457,423,222,1179,0

1821,843,422,3262,10

1255,1184,625,3298,12

2598,2197,1076,6285,13

1070,526,314,1966,2

...

Sygnały możesz zebrać uruchamiając sorter z moją siecią NN np. w programie Realterm z opcją Capture do pliku tekstowego i podmienić indeks koloru w swoich danych na indeks koloru koralików, które aktualnie mierzysz.

Po przygotowaniu danych należy je podmienić w pliku pearlers_data.txt w katalogu z kodem MAIN_beadsSorterNN.m i uruchomić program. Po zakończeniu treningu w katalogu wynikowym bsNN_outputs pojawi się plik NN_code.c, którego zawartość należy wkleić w odpowiednim miejscu w kodzie Sorter.ino (nadpisując poprzednie dane) i załadować do sortera. Brawo! Masz własną wyszkoloną sieć do sortowania swoich koralików!!

Miłego sortowania!

Pliki do pobrania (downloads)

1. Kod arduino: Sorter.ino 

2. kod Octave: MAIN_beadsSorterNN.zip

3. pliki do druku do porania na Thingiverse